|
アーチェリーの的は直径８０ｃｍ（６０ｍ以上の距離は直径１２２ｃｍ）で、そこを同心円で１０個の得点帯に区切っている。中心の直径８ｃｍの円がもっとも高い１０点、そこから直径１６ｃｍ以内までが９点‥‥直径７８ｃｍから８０ｃｍの間が１点という形だ。
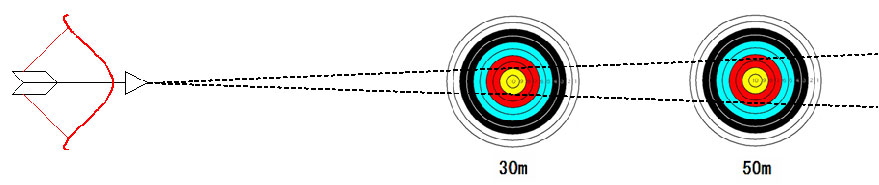
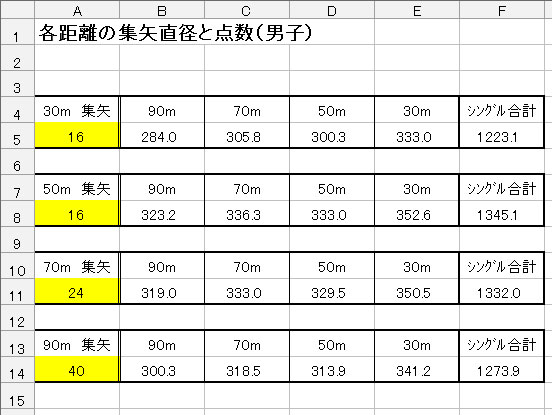
ということは、すべての矢を直径８ｃｍ以内に収めることができれば満点（３６０点）が取れるわけだ。 （ちなみに２０１２年現在、最短距離である３０ｍでの日本記録は３５８点） しかし、そう簡単に日本新記録が出せるわけではない。では９点の直径１６ｃｍの範囲であればどうだろうか？ 仮に、射た矢がすべて的の中心の直径１６ｃｍの円の中に均等に刺さったとする（今後、これを集矢直径と勝手に定義する）。 直径１６ｃｍの９点の中に直径８ｃｍの１０点があるので、一部の矢は１０点に刺さる。そして、１０点に刺さる矢とと９点に刺さる矢の割合は的上での面積の割合できまる。 |
|
|
この場合、１０点：９点は１：３となるので、矢を３６本射たとすると１０点９本と９点２７本で合計３３３点ということになる。
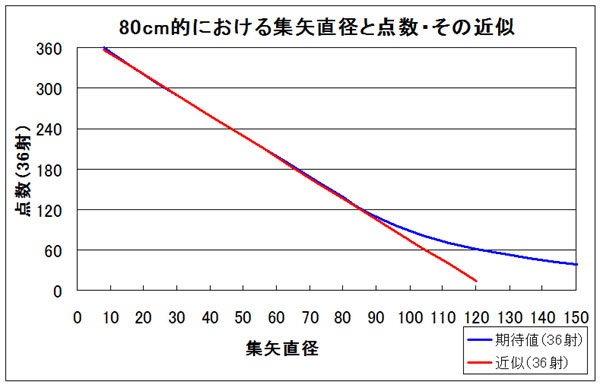
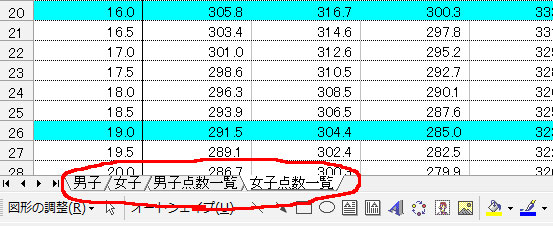
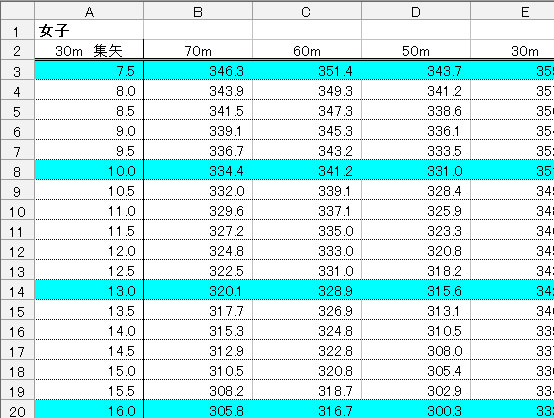
同様のことを８点（２４ｃｍ）まで、７点（３２ｃｍ）までと考えていくと右のグラフの青い線のようになる。 その線に重なるようにして赤い直線を引くと、見てのとおり集矢直径が１０ｃｍ〜８０ｃｍの間はほぼ直線的に点数が変化していくことがわかる。そこでこの直線を近似値として式を立てると Ｐ：３６射での予測点数 ２Ｒ ： 集矢直径 |
|
|
さらに、長距離（男子７０ｍ９０ｍ、女子６０ｍ７０ｍ）では的の直径が１２２ｃｍに変わることも考慮に入れれば 一つの距離での集矢直径が分かればすべての距離での点数が当然すべて計算できることになる。
ということで完成品（？）がこれだ→ 黄色の枠の中に指定の距離での集矢直径を入れると、自動的にシングル（※）各距離の点数とその合計が計算される。 高校や大学のアーチェリー場は、初心者と一緒に練習したり、広さが足りなかったりする関係で長距離を使えないことが多い。 しかし、これを使えば今練習できる距離での集矢直径から、任意の距離やシングル全体の点数が大雑把にとはいえ、分かることになる。 （※シングル：全日本選手権や世界選手権などで使われる試合形式で、男子90m70m50m30m、女子70m60m50m30mの４距離３６射ずつの合計点数（1440点満点）で争う。日本では1350点くらい出すとオリンピック選手になれる） |
|
|
下のタブで切り替えると女子の場合も計算することができる。
ついでなので、３０ｍでの集矢直径を５ｍｍ毎に点数を計算したリストも入れてみた。 |
|
|
これを見れば、自分のシングルの目標点数に対して、普段の練習距離では何点程度出す必要があるのか目安を付けることができる。
また、 『３０ｍでの集矢直径を約2.5ｃｍ縮めるとシングルの点数が約５０点上がる』 だとか、 『３０ｍで直径１７ｃｍの円の中にすべての矢が入るようになれば１２００点が出る』 という形で練習の目標に使ったり、指導に役立てたりすることも出来るだろう。 使い方次第でいろいろなことが出来そうな予感がする。 例によって、これについて著作権は主張しない。個人で使おうが、学校で使おうが、さらに改善を施そうが自由だが、もらっていく旨を掲示板なり、メールなりで教えてもらえると大変ありがたい。 |
|
| SEO | [PR] 爆速!無料ブログ 無料ホームページ開設 無料ライブ放送 | ||
